上半部分请参见 《排序算法一览(上):交换类、选择类和插入类排序》。
归并类排序
归并排序(Merge Sort)
归并排序是一种分治法,它反复将两个已经排序的序列合并成一个序列(平均时间复杂度 O(nlogn),最好时间复杂度 O(n)):
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
- 重复步骤直到某一指针达到序列尾;
- 将另一序列剩下的所有元素直接复制到合并序列尾。
public class Sort {
public static > void mergeSort( T[] arr ) {
T[] tmpArr = (T[]) new Comparable[arr.length];
mergeSort(arr, tmpArr, 0, arr.length - 1);
}
private static >
void mergeSort( T[] arr, T[] tmpArr,
int left, int right ) {
//recursive way
if ( left < right ) {
int center = ( left + right ) / 2;
mergeSort(arr, tmpArr, left, center);
mergeSort(arr, tmpArr, center + 1, right);
merge(arr, tmpArr, left, center + 1, right);
}
}
private static > void merge( T[] arr, T[] tmpArr,
int lPos, int rPos, int rEnd ) {
int lEnd = rPos - 1;
int tPos = lPos;
int leftTmp = lPos;
while ( lPos <= lEnd && rPos <= rEnd ) {
if ( arr[lPos].compareTo( arr[rPos] ) <= 0 )
tmpArr[ tPos++ ] = arr[ lPos++ ];
else
tmpArr[ tPos++ ] = arr[ rPos++ ];
}
//copy the rest element of the left half subarray.
while ( lPos <= lEnd )
tmpArr[ tPos++ ] = arr[ lPos++ ];
//copy the rest elements of the right half subarray. (only one loop will be execute)
while ( rPos <= rEnd )
tmpArr[ tPos++ ] = arr[ rPos++ ];
//copy the tmpArr back cause we need to change the arr array items.
for ( ; rEnd >= leftTmp; rEnd-- )
arr[rEnd] = tmpArr[rEnd];
}
}

归并排序有许多变种,比如梯级归并排序(Cascade Merge Sort)、振荡归并排序(Oscillating Merge Sort)和多相归并排序(Polyphase Merge Sort)。以多相归并排序为例,它经常用在外排序中,可以减少原始归并排序每次循环需要遍历的元素个数,因为原始的归并排序每次都做二路归并,在文件数量多的时候效率低下。
Strand 排序(Strand Sort)
Strand 排序不断地从待排序的序列中拉出排好序的子列表,并归并成一个最终的结果。该算法的平均和最坏时间复杂度都达到了 O(n2),最好时间复杂度为 O(n)。Strand 排序高效的条件要求:
- 以链表(linked list)方式存放的数据排序起来最为有效,因为它需要反复添加和移除元素,而链表添加移除元素的代价很小;
- 原始数据中已经很大程度上有序了,这样每次可以尽量多地拉出一个有序子列表数据。
举例来说,现在有原始列表(4,5,2,3,1):
- 遍历元素,第一个元素 4,拉出包含 4 的最长递增子序列:(4,5),原列表变成了(2,3,1);
- 继续拉出最长递增子序列(2,3),和前面拉出的序列归并得到(2,3,4,5),原列表变成了(1);
- 拉出(1),归并得到(1,2,3,4,5)。
procedure strandSort( A : list of sortable items ) defined as:
while length( A ) > 0
clear sublist
sublist[ 0 ] := A[ 0 ]
remove A[ 0 ]
for each i in 0 to length( A ) - 1 do:
if A[ i ] > sublist[ last ] then
append A[ i ] to sublist
remove A[ i ]
end if
end for
merge sublist into results
end while
return results
end procedure
分布类排序
基数排序(Radix Sort)
相较于前面严格的比较排序,基数排序更多地利用了待排序元素本身的特性。待排序元素需要是整型,基数排序时将整数按照位数切分成不同的数字,然后按每个位数分别比较;但是推广一下,整数也可以表达字符串,和符合特定格式的浮点数,所以基数排序堆元素的要求进一步降低。具体实现步骤:
待比较元素统一成相同格式(例如短数前面补零),然后从最低位开始,依次进行一次排序,接着是次低位……直到最高位也完成排序。
例如有元素(432,546,723):
- 第一遍按照个位数排序,变成(432,723,546);
- 接着按照十位数排序:(723,432,546);
- 最后是百位数:(432,546,723)。
基数排序的时间复杂度是 O(k*n),其中 n 是待排序元素个数,k 是数字的位数,它的复杂度理论上要低于 O(n*logn),但是如果考虑到实际上 k 也和 n 存在关系,那就不是这样了。就以排序 n 个不同的整数为例,每一位都有 0-9 这 10 个不同的数字,所以 10 的 k 次方必须大于等于 n,所以 k≥log10n。所以按照这个角度来说,它的时间复杂度还是在 O(n*logn)。
const int base=10;
wx *headn,*curn,*box[base],*curbox[base];
void basesort(int t)
{
int i,k=1,r,bn;
for(i=1;i<=t;i++)
{
k*=base;
}
r=k*base;
for(i=0;inext;curn!=NULL;curn=curn->next)
{
bn=(curn->num%r)/k;
curbox[bn]->next=curn;
curbox[bn]=curbox[bn]->next;
}
curn=headn;
for(i=0;inext=box[i]->next;
curn=curbox[i];
}
}
curn->next=NULL;
}
int main()
{
int i,n,z=0,maxn=0;
curn=headn=new wx;
cin>>n;
for(i=0;inext=new wx;
cin>>curn->num;
maxn=max(maxn,curn->num);
}
while(maxn/base>0)
{
maxn/=base;
z++;
}
for(i=0;i<=z;i++)
{
basesort(i);
}
printwx();
return 0;
}
美国旗帜排序(American Flag Sort)
美国旗帜排序是基数排序的一种原地排序变种,和原始的基数排序一样,只能排数字,或者是能用数字表示的对象,而它原地排序的特性,节约了空间消耗和数组拷贝开销。美国旗帜排序把元素归类到若干个桶里面,经常用来给大对象排序,比如字符串(如果给大字符串使用比较排序,时间复杂度过高)。加上一定的优化以后,对于一大组字符串的排序,时间消耗可以接近快排。步骤基本上可以表示为:
- 根据最高位的基数划分桶并在数组上找到每个桶的边界;
- 通过交换把元素放置到正确的桶中;
- 在每个桶中继续使用美国旗帜排序。
伪代码如下:
american_flag_sort(Array, Radix)
for each digit D:
# first pass: compute counts
Counts <- zeros(Radix)
for object X in Array:
Counts[digit D of object X in base Radix] += 1
# compute bucket offsets
Offsets <- [ sum(Counts[0..i]) for i in 1..Radix]
# swap objects into place
for object X in Array:
swap X to the bucket starting at Offsets[digit D of X in base Radix]
for each Bucket:
american_flag_sort(Bucket, Radix)
珠排序(Bead Sort)
珠排序是自然排序算法的一种,时间复杂度在 O(n),缺点是空间复杂度始终需要 O(n2),而且,和传统基数排序一样,要求排序对象可以用有限整数来表示。珠排序的过程非常容易理解:

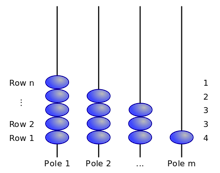
每一行表示一个数,从左往右排列珠子,有珠子的列的个数表示了数的值。排好后珠子随重力下落,获得排序结果。
桶排序(Bucket Sort)
桶排序也叫做箱排序,把待排序元素分散到不同的桶里面,每个桶再使用桶排序再分别排序(和前面提到的美国旗帜排序差不多,只不过这里需要额外的空间来放置桶,而且放置元素到桶中的过程也不采用美国旗帜排序中的元素交换):
function bucket-sort(array, n) is
buckets ← new array of n empty lists
for i = 0 to (length(array)-1) do
insert array[i] into buckets[msbits(array[i], k)]
for i = 0 to n - 1 do
next-sort(buckets[i])
return the concatenation of buckets[0], ..., buckets[n-1]
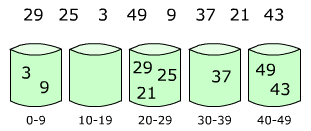
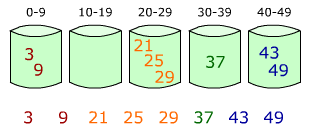
上面两张图中,左图是第一步,给元素分到不同的桶中;右图是给每个桶中的元素继续排序。
鸽巢排序(Pigeonhole Sort)
鸽巢排序也被称作基数分类,是一种时间复杂度为 O(n),且在不可避免地遍历每一个元素并且已经排序的情况下效率最好的一种排序算法。但它只有在差值(或者可被映射在差值)很小的范围内的数值排序的情况下实用。当涉及到多个不相等的元素,且将这些元素放在同一个 “鸽巢” 的时候,算法的效率会有所降低。
for i in [0...length(a)-1]
b[a[i]] := b[a[i]]+1
j := 0
for i in [0...length(b)-1]
repeat b[i] times
a[j] := i
j := j+1
以一个例子来解释上述伪代码:
待排序数列 a:(2,3,2,4,3,1,5),那么辅助数列 b,b[x] 表示数列 a 中值为 x 的元素个数,于是 b 就为 (0,1,2,2,1,1),最后得到排序后的数列:(1,2,2,3,3,4,5)。
相邻图排序(Proxmap Sort)
相邻图排序源于基础的桶排序和基数排序,在把待排序元素划分成若干个桶的时候,这个划分规则是通过一个相邻图给出的,并且在将元素放入桶内的过程,是通过插入排序来完成的,如果这个划分得当,排序可以接近线性的复杂度。在数据量增大的情况下这个算法性能表现不错。
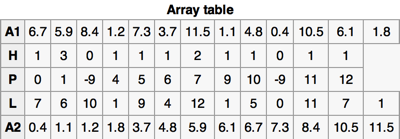
以一个例子,借助上面的图,如果待排序数组 A,它的 key 有 n 个,现在把算法描述一下:
- 确定有多少个键会映射到同一个子数组,这一步需要使用一个 “hit count”(H)的辅助数组;
- 确定每个子数组在 A2 中的位置,这一步需要使用辅助数组 “proxmaps”(P);
- 对于每一个 key,计算得到将被映射到哪一个子数组中,这个信息存放在辅助数组 “locations”(L)中;
- 对于每一个 key,根据它的 location,把它放到 A2 中,A2 中已经有这个 key 了,那就变成一次插入操作,把比它大的元素后移。

计数排序(Counting Sort)
计数排序是一种稳定的排序算法。计数排序使用一个额外的数组 C,其中第 i 个元素是待排序数组 A 中值等于 i 的元素的个数。然后根据数组 C 来将 A 中的元素排到正确的位置。当输入的元素是 n 个 0 到 k 之间的整数时,它的运行时间是 O(n + k)。计数排序不是比较排序,排序的速度快于任何比较排序算法。
private static void countingSort(int[] A, int[] B, int k) {
int[] C = new int[k];
// 计数
for (int j = 0; j < A.length; j++) {
int a = A[j];
C[a] += 1;
}
// 求计数和
for (int i = 1; i < k; i++) {
C[i] = C[i] + C[i - 1];
}
// 整理
for (int j = A.length - 1; j >= 0; j--) {
int a = A[j];
B[C[a] - 1] = a;
C[a] -= 1;
}
}
混合类排序
Tim 排序是一种结合了归并排序和插入排序的混合排序法,算法首先寻找数据的有序子数组(被称作 “run”),并且利用这个知识来提高排序效率(比如低于某个阈值会使用插入排序技术等等),然后要对有序子数组进行归并,持续这样的操作直到条件满足,排序结束。值得一提的是,它在 JDK 7 中被用来给默认非原语类型的数组排序。
这个排序算法首先从快速排序开始,当递归深度超过一定深度(深度为排序元素数量的对数值)后转为堆排序。采用这个方法,自省排序既能在常规数据集上实现快速排序的高性能,又能在最坏情况下仍保持 O(n*logn) 的时间复杂度。
Spread 排序结合了基于分布的排序(比如桶排序和基数排序),并且引入比较排序(比如快速排序和归并排序)中的分区概念,在实验中表现出来的效果要好过传统的排序方法。快排的主要理念是找到一个中心元素(pivot)然后分成前后两个子列表,一个元素都小于等于 pivot,一个元素都大于等于 pivot;Spread 排序则是划分成 n/c 的(n 是元素个数,c 是一个较小的常量)分区(被称为 bin),然后使用基于分布的排序来完成,这其中会使用启发式的测试来确定对于 bin 递归排序的过程使用哪一种排序算法。
UnShuffle 排序是一种分布排序和归并排序的结合,它在数据的熵值非常低(数据相对有序,比如基本有序或者包含大量有序子串)的时候最有效。排序过程分为两个步骤:
- 1、分布排序阶段,通过最小次数的比较,待排序元素被分发到一些子列表中;
- 2、每一个子列表的排序结果会被归并到最终结果中去。
J 排序是通过构建两次堆(一次小根堆,一次大根堆)来让数列大致有序,接着再使用插入排序来完成的原地排序算法。
文章未经特殊标明皆为本人原创,未经许可不得用于任何商业用途,转载请保持完整性并注明来源链接 《四火的唠叨》
非常好