
只是记录一下遇到的几道抛硬币的概率问题。
1、平均需要抛掷多少次硬币,才会首次出现连续的两个正面?
假设连续两个正面的期望是 E,那么,先看第一次抛硬币:
- 如果抛到反面,那么还期望抛 E 次,因为抛到反面完全没用,总数就期望抛 E+1
- 如果抛到正面,那么要看下一次,如果下一次也是正面,那抛硬币就结束了,总数是 2;如果下一次是反面,那么相当于重头来过,总数就期望抛 E+2
于是可以得到如下关系式:
E = 0.5(E+1) + 0.25*2 + 0.25(E+2)
得到所求期望 E=6
现在把题目拓展,不是说 “连续两个正面”,而是 “连续 n 个正面” 呢?
这个问题 Matrix67 有非常有趣的解答 《用数学解赌博问题不稀奇,用赌博解数学问题才牛 B》,下面我简述一下:
假设有一个赌场,赌博的方式就是猜正反,每来一个玩家来的时候都只带了 1 元,每次都会全部下注,然后赌正面,庄家抛硬币,如果猜错就是全部输掉,如果赢了就得到下注的两倍,玩家会一直玩一直玩直到钱输光;而赌场老板会看,如果有人赢到 2^n 元,就下令关闭赌场。
于是直到 n 次正面朝上的情况发生,赌场关闭,只有最后那 n 个人才赚到了钱,最后一人得到了 2 元(没算成本价 1 元),倒数第二人是 4 元……倒数第 n 人是 2^n 元,所以,一共得到(等比数列求和):
2+4+8+…+2^n = 2*(1-2^n)/(1-2) = 2^(n+1) – 2
赌场有多少钱流入,自然就有多少钱流出,所以到赌场倒闭,玩家赢得的钱的总数,就应该等于赌场期望的收入。而因为每个人来的时候都只带了 1 元,因此这个数正好等于期望的人数。于是这就是最终答案。
2、一堆硬币,每天都随便捡一枚抛,如果抛到正面,就把它翻过来;如果抛到反面,就再抛一下,问很长很长时间以后,硬币正面和反面的比例会趋近于多少?
假设正面的比例是 x,那么反面就是 1-x,对于任意一次操作:
- 如果抛到正面,那么得到的就一定是反面了;
- 如果抛到反面,那么得到正面的可能性为 0.5,反面的也为 0.5。
所以得到正面的综合起来的概率为:
x*0 + (1-x)*0.5 = x
所以 x = 1/3,因此硬币正面和反面的比例会趋近于 x/(1-x) = 1/2
3、连续抛硬币,直到第一次出现连续两次正面为止,恰好抛了 N 次的概率是多少?
考虑 “恰好” 抛 N 次硬币,到底有多少种情况可以得出最后两次是连续出现了正面,而之前没有出现过连续正面。
- 假设 f(x) 表示第一次出现连续正面的时候,已经抛了 x 次,并且整个过程的第一次抛出的结果是反面;
- 假设 g(x) 表示第一次出现连续正面的时候,已经抛了 x 次,并且整个过程的第一次抛出的结果是正面。
所以 f(1)=f(2)=0,g(1)=0,g(2)=1,而当 x>2,
- 求 f(x+1),因为第一次是反面,所以这新添加的第一次不影响结果,因此 f(x+1)=f(x)+g(x)
- 求 g(x+1),因为第一次是正面,必须要保证第二次不能为正,所以 g(x+1)=f(x)
于是得到:
f(x+2)=f(x+1)+g(x+1)=f(x+1)+f(x)
g(x+1)=f(x)
其中,求 f(x) 的递推式可以看出 f(x) 是斐波那契数列,根据它的通项公式:
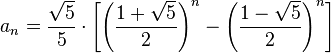
得到 f(N),也就得到了 g(N),而总抛的可能性共有 2^N 次方,因此,概率为:
(f(N)+g(N))/2^N
4、抛硬币 N 次,出现连续 M 次正面的概率是多少?
这个问题也很常见,但是做起来没那么容易,这里有一个非常详细的讨论过程(链接),我就不搬过来了。
5、抛 N 次硬币,正反两面出现次数相同的概率是多少?
其实就是从 N 个硬币的空位中,选出 N/2 个作为正面,余下 N/2 个作为反面,应用组合公式可得到:
C(N,N/2)/2^N=N!/((N-N/2)!(N/2)!)/2^N
继续,
正面出现次数超过反面的概率?
因为正反情况相同,因此正面次数超过反面的概率应当等于反面次数超过正面的概率,因此结果为 1 减去上面那一问的结果之后除以 2:
(1-C(N,N/2)/2^N)/2
文章未经特殊标明皆为本人原创,未经许可不得用于任何商业用途,转载请保持完整性并注明来源链接 《四火的唠叨》