α 和β 均大于零,且令λ=1/β,假设 X 的密度满足:
就说 X 是服从参数为 (β,α) 的 Gamma 分布,记为Γ(β,α)。Gamma 分布的两个参数中,第一个β 决定了形状 (shape),第二个参数α 决定了尺度 (scale)。
右上图中的 k 即是α,θ 即是β;期望 E=β/α,方差 D=β/(α*α)。曲线有一个峰,左右不对称。在α 比较大时,曲线接近于正态分布。
Erlang 分布
当β 为正整数 n 的时候,那么λ=1/n,Γ(n,α) 满足 Erlang 分布。Erlang 分布经常用来表示独立随机事件发生的时间间隔。比如一个车站从第一辆车到达,直到恰好有 n 辆车到达所需要的时间分布。
Erlang 分布有两个参数:k 表示阶数 (stage),μ 表示均值。概率密度符合:
概率密度符合 k 阶 Erlang 分布。
指数分布
当β=1 时,Γ(1,α) 表示参数为α 的指数分布 exp(α)。指数分布也经常用来表示独立随机事件发生的间隔,电子产品的寿命分布一般服从指数分布。指数分布不具备记忆性,如果一个人活了六十年,他再活十年的概率和一个十岁的孩子再活十年的概率,通常来说后者要高得多,这种情况就是记忆性的体现,不可能服从指数分布。
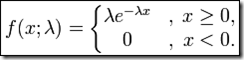
它的概率密度函数:
卡方分布
当α =n/2 ,β=1/2 时,Γ(n/2,1/2) 即是χ2 分布(卡方分布)。n 个相互独立的随机变量,均服从正态分布,那么这 n 个随机变量的平方和构成的新随机变量,分布规律符合χ2(n) 分布。所以卡方分布曲线下总面积为 1,x 取负值没有意义。
它的概率密度函数:
文章未经特殊标明皆为本人原创,未经许可不得用于任何商业用途,转载请保持完整性并注明来源链接 《四火的唠叨》

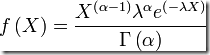
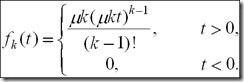
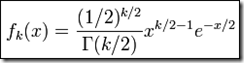
这个有点晕啊,alpha 和 beta 貌似反了,Gamma 分布是不是写反了?
而均值,方差的公式也错了,卡方也错了,同学你是不是故意的。。。。
这是我搞糊涂了。卡方没错误。
居然整个把 alpha,beta 反着说。。。。。。。